Tag: Exponential Idle

Weierstrass Sine Product, qdot simulator.

%Matthew Miller
%v_4
%2/8/22
%Calculates max qdot for a range of n and c1 values
%to do more I’d have to optimize a time-dependent progression
%I may do it later

%pdot = q1*q2*q
%qdot = m3Factor * s_n(chi)/sin(chi)
%s_n(chi) = chi * PI(k=1:n)(1-(chi/(k*pi))^2)

%==========================================================================
%start fresh

clear all

%==========================================================================
%human entry

%set number of purchases
steps = 1000;

%since the maximum number of purchases of each variable is all of the
%purchases, these can be set to steps
nDimension = steps;
c1Dimension = steps;

%not sure what to do with these yet
q1=1;
q2=1;
c2=1;

m1=4; %Milestone upgrade 1 level (0, 1, 2, 3, or 4)
m2=1; %Milestone upgrade 2 level (0 or 1)
m3=3; %Milestone upgrade 3 level (0, 1, 2, or 3)

%==========================================================================
%prelim calculations

nIndex=1:nDimension; %X axis
c1Index=1:c1Dimension; %Y axis

m1Factor = q1^(1+0.01*m1); %precalculate
m2Factor = c2^m2; %precalculate
m3Factor = 3^m3; %precalculate

chi = zeros(nDimension,c1Dimension); %preallocate for speed
sinterm = zeros(nDimension,c1Dimension); %preallocate for speed
s_n = zeros(nDimension,c1Dimension); %preallocate for speed
qdot = zeros(nDimension,c1Dimension); %preallocate for speed

%==========================================================================
%generate variables
%Normally I’d do all these with functions, but that’s harder to read

%blah blah blah arrays begin at 1 so I’m ignoring c1(0)=0

stepLength = 50;
basePower = 1;
offset = 1;

power=basePower;
c1steps=1;

c1(1)=offset;

for index = 2:c1Dimension
c1(index) = c1(index-1)+power;
c1steps=c1steps+1;
if c1steps > stepLength
power=power*2;
c1steps=1;
end
end

%chi
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
chi(n_index,c1_index) = pi.*c1(c1_index).*nIndex(n_index)./(c1(c1_index)+nIndex(n_index)/m3Factor)+1; %x=n, y=c1
end
end

%sin(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
sinterm(n_index,c1_index) = sin(chi(n_index,c1_index));
end
end

%s_n(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
s_n(n_index,c1_index) = chi(n_index,c1_index);
s_nk(1)=chi(n_index,c1_index)*(1-(chi(n_index,c1_index)/(1*pi))^2);
if n_index>1
for k = 2:n_index %Big Pi
s_nk(k)=s_nk(k-1)*(1-(chi(n_index,c1_index)/(k*pi))^2);
end
end
s_n(n_index,c1_index)=s_nk(end);
end
end

%qdot(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
qdot(n_index,c1_index)=m2Factor*s_n(n_index,c1_index)/sinterm(n_index,c1_index);
end
end

[M,I] = max(qdot(:));
[n_max, c1_max] = ind2sub(size(qdot),I); %Maximum values
qdot(n_max,c1_max);

%========================================================================================
%plotter
%========================================================================================

clear rows cols

maxSteps = steps;
minSteps = 1;
for stepsIndex=minSteps:maxSteps

nRange=stepsIndex;
c1Range=stepsIndex;

C=max(qdot(1:nRange,1:c1Range));
D=max(C);
[rows(stepsIndex), cols(stepsIndex)] = find(qdot(1:nRange, 1:c1Range) == D);

end

figure(1)
plot(rows, cols)
title(‘Peak Qdot’)
xlabel(‘n’)
ylabel(‘c1’)

Without cost, the best purchase works out to be linear. There’s no cool backstepping or ommissions worth chasing.

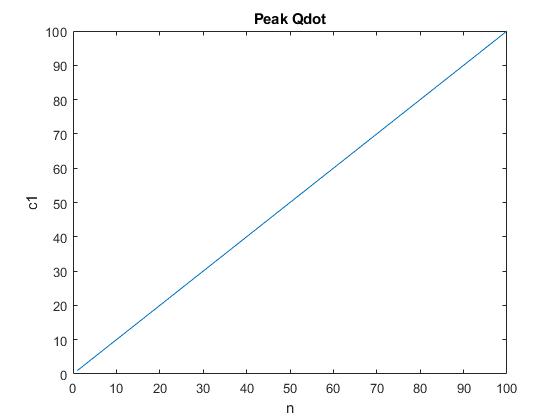
I’m hunting around for typos, but it seems to match up with the game results pretty carefully. Perhaps including a cost function, there will be a way to beat the autobuyer.