Weierstrass Sine Product, qdot simulator.
%Matthew Miller
%v_4
%2/8/22
%Calculates max qdot for a range of n and c1 values
%to do more I’d have to optimize a time-dependent progression
%I may do it later
%pdot = q1*q2*q
%qdot = m3Factor * s_n(chi)/sin(chi)
%s_n(chi) = chi * PI(k=1:n)(1-(chi/(k*pi))^2)
%==========================================================================
%start fresh
clear all
%==========================================================================
%human entry
%set number of purchases
steps = 1000;
%since the maximum number of purchases of each variable is all of the
%purchases, these can be set to steps
nDimension = steps;
c1Dimension = steps;
%not sure what to do with these yet
q1=1;
q2=1;
c2=1;
m1=4; %Milestone upgrade 1 level (0, 1, 2, 3, or 4)
m2=1; %Milestone upgrade 2 level (0 or 1)
m3=3; %Milestone upgrade 3 level (0, 1, 2, or 3)
%==========================================================================
%prelim calculations
nIndex=1:nDimension; %X axis
c1Index=1:c1Dimension; %Y axis
m1Factor = q1^(1+0.01*m1); %precalculate
m2Factor = c2^m2; %precalculate
m3Factor = 3^m3; %precalculate
chi = zeros(nDimension,c1Dimension); %preallocate for speed
sinterm = zeros(nDimension,c1Dimension); %preallocate for speed
s_n = zeros(nDimension,c1Dimension); %preallocate for speed
qdot = zeros(nDimension,c1Dimension); %preallocate for speed
%==========================================================================
%generate variables
%Normally I’d do all these with functions, but that’s harder to read
%blah blah blah arrays begin at 1 so I’m ignoring c1(0)=0
stepLength = 50;
basePower = 1;
offset = 1;
power=basePower;
c1steps=1;
c1(1)=offset;
for index = 2:c1Dimension
c1(index) = c1(index-1)+power;
c1steps=c1steps+1;
if c1steps > stepLength
power=power*2;
c1steps=1;
end
end
%chi
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
chi(n_index,c1_index) = pi.*c1(c1_index).*nIndex(n_index)./(c1(c1_index)+nIndex(n_index)/m3Factor)+1; %x=n, y=c1
end
end
%sin(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
sinterm(n_index,c1_index) = sin(chi(n_index,c1_index));
end
end
%s_n(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
s_n(n_index,c1_index) = chi(n_index,c1_index);
s_nk(1)=chi(n_index,c1_index)*(1-(chi(n_index,c1_index)/(1*pi))^2);
if n_index>1
for k = 2:n_index %Big Pi
s_nk(k)=s_nk(k-1)*(1-(chi(n_index,c1_index)/(k*pi))^2);
end
end
s_n(n_index,c1_index)=s_nk(end);
end
end
%qdot(chi)
for n_index=1:nDimension %X
for c1_index=1:c1Dimension %Y
qdot(n_index,c1_index)=m2Factor*s_n(n_index,c1_index)/sinterm(n_index,c1_index);
end
end
[M,I] = max(qdot(:));
[n_max, c1_max] = ind2sub(size(qdot),I); %Maximum values
qdot(n_max,c1_max);
%========================================================================================
%plotter
%========================================================================================
clear rows cols
maxSteps = steps;
minSteps = 1;
for stepsIndex=minSteps:maxSteps
nRange=stepsIndex;
c1Range=stepsIndex;
C=max(qdot(1:nRange,1:c1Range));
D=max(C);
[rows(stepsIndex), cols(stepsIndex)] = find(qdot(1:nRange, 1:c1Range) == D);
end
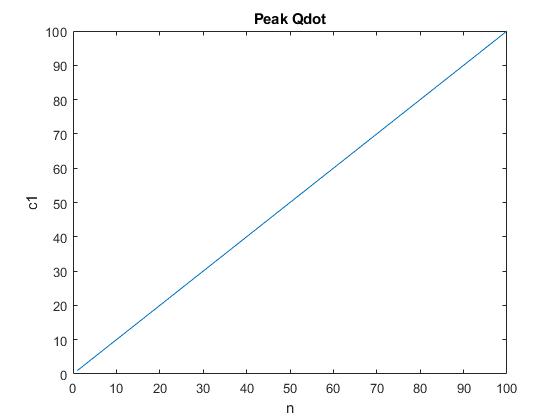
figure(1)
plot(rows, cols)
title(‘Peak Qdot’)
xlabel(‘n’)
ylabel(‘c1’)